算法图库与表格汇总

图片请与本 HTML 放在同一目录；点击缩略图可放大预览。

1) 图库（按主题分类）

如果某一类暂时没有图片，会显示“暂无图片”。

归并排序

归并排序1.png

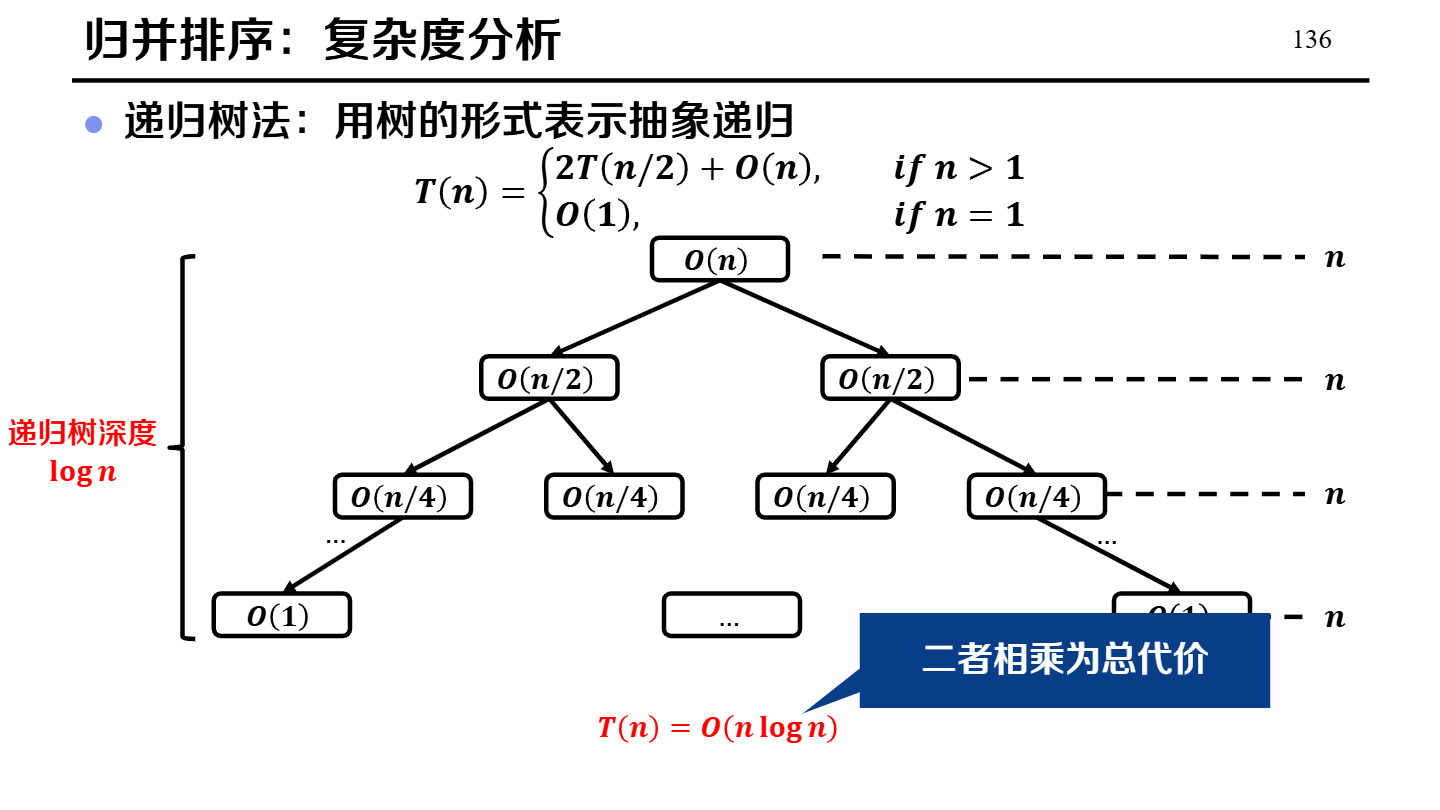
归并排序递归树.png

归并排序复杂度.png

归并排序伪代码.png

选择排序

暂无图片（如果你之后把“选择排序xxx.png”放进同目录，可在 HTML 中按同样格式补上）。

LCS 填表

LCS初始化.png

LCS打印.png

LCS动态规划.png

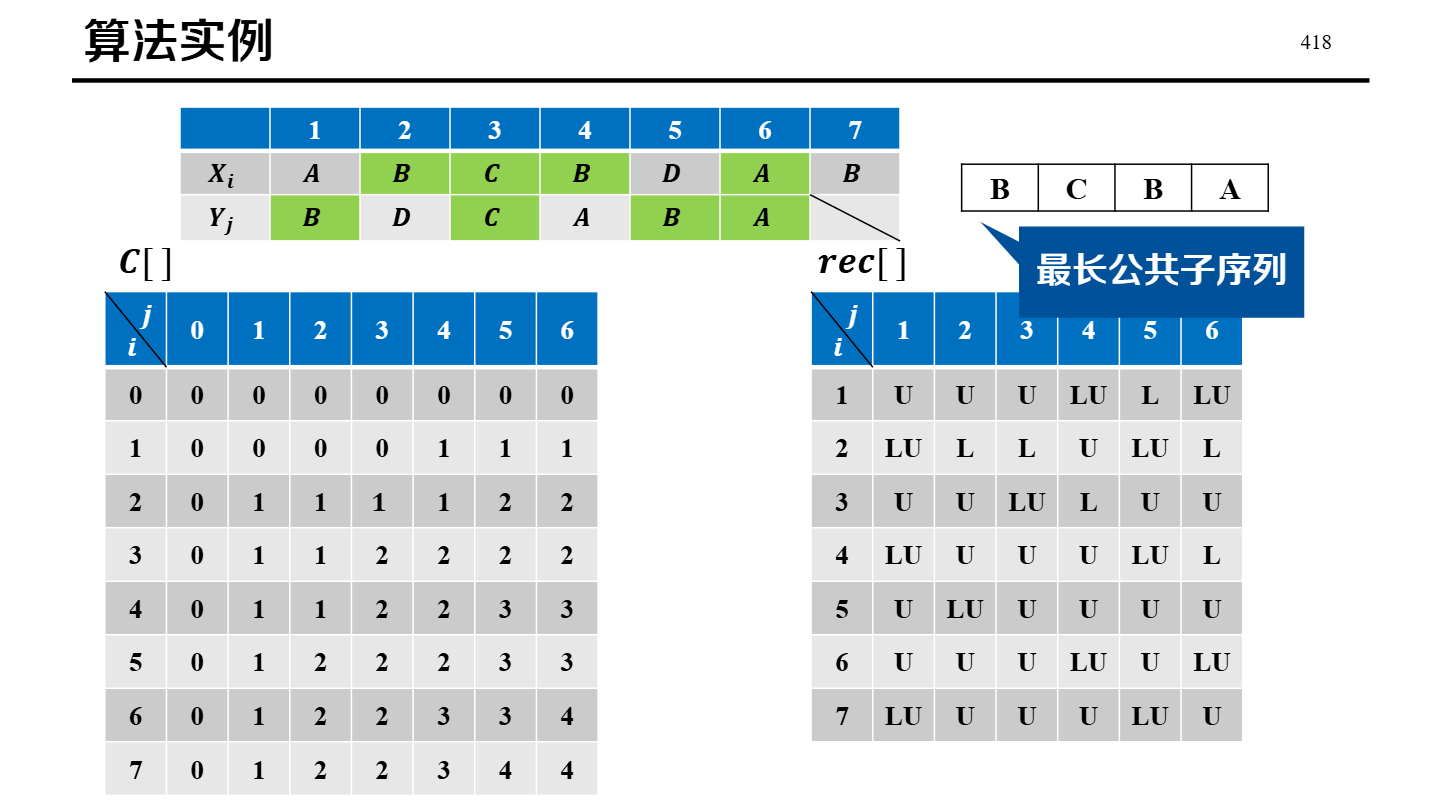
最长公共子序列示例.png

MST 构造（Prim / Kruskal）

Kruskal

MST概念.png

kruskal算法思想.png

kruskal示例.png

kruskal伪代码.png

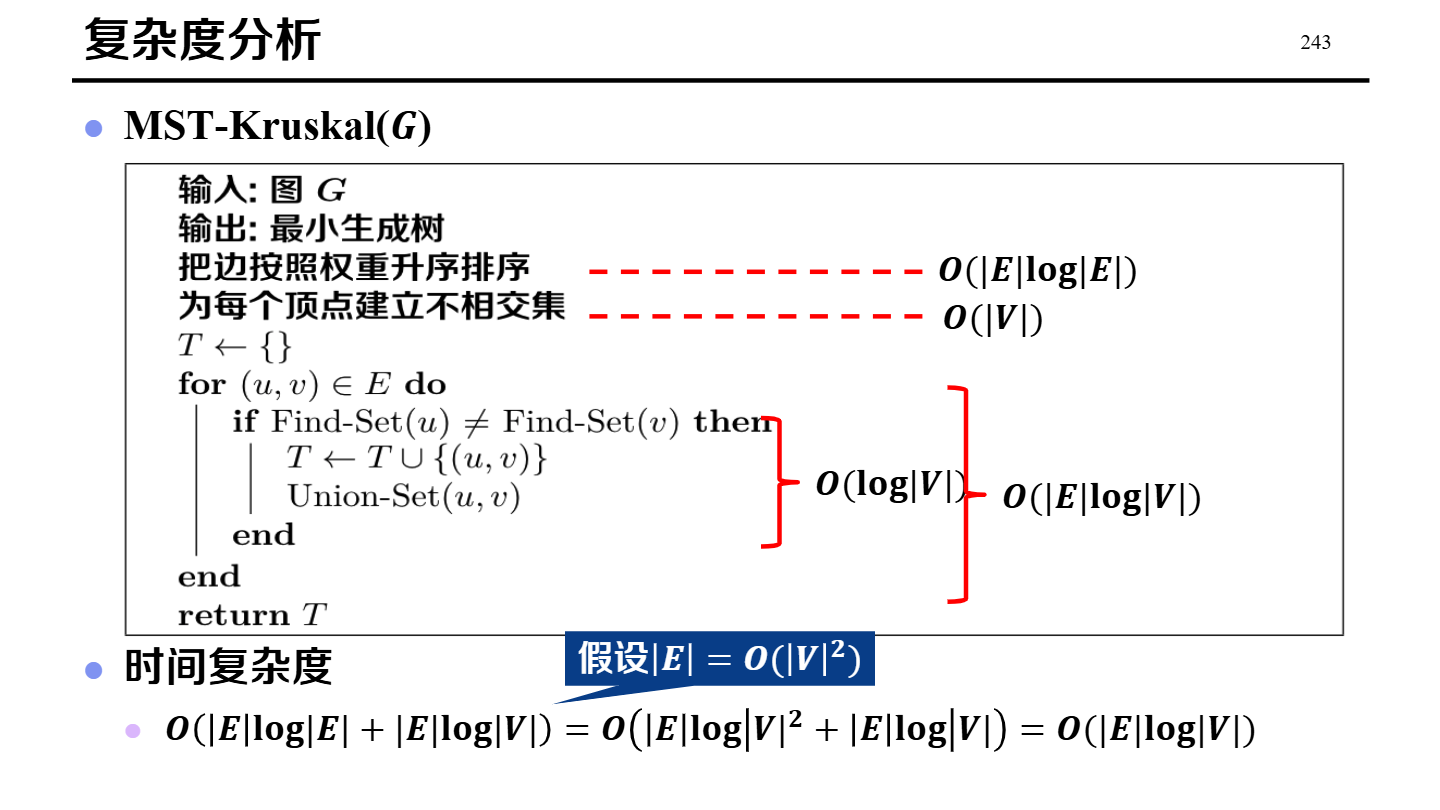
kruskal复杂度.png

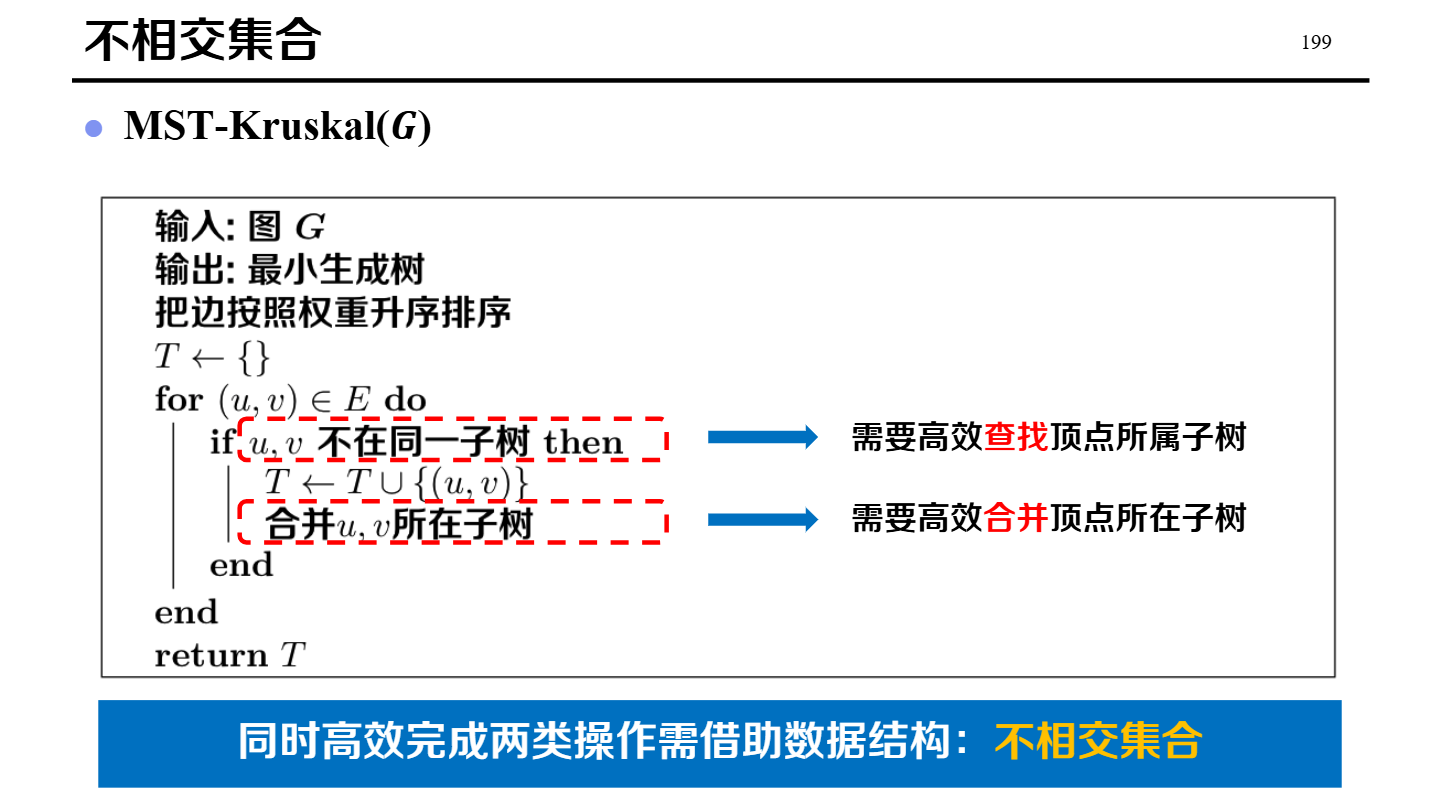
kruskal不相交集合.png

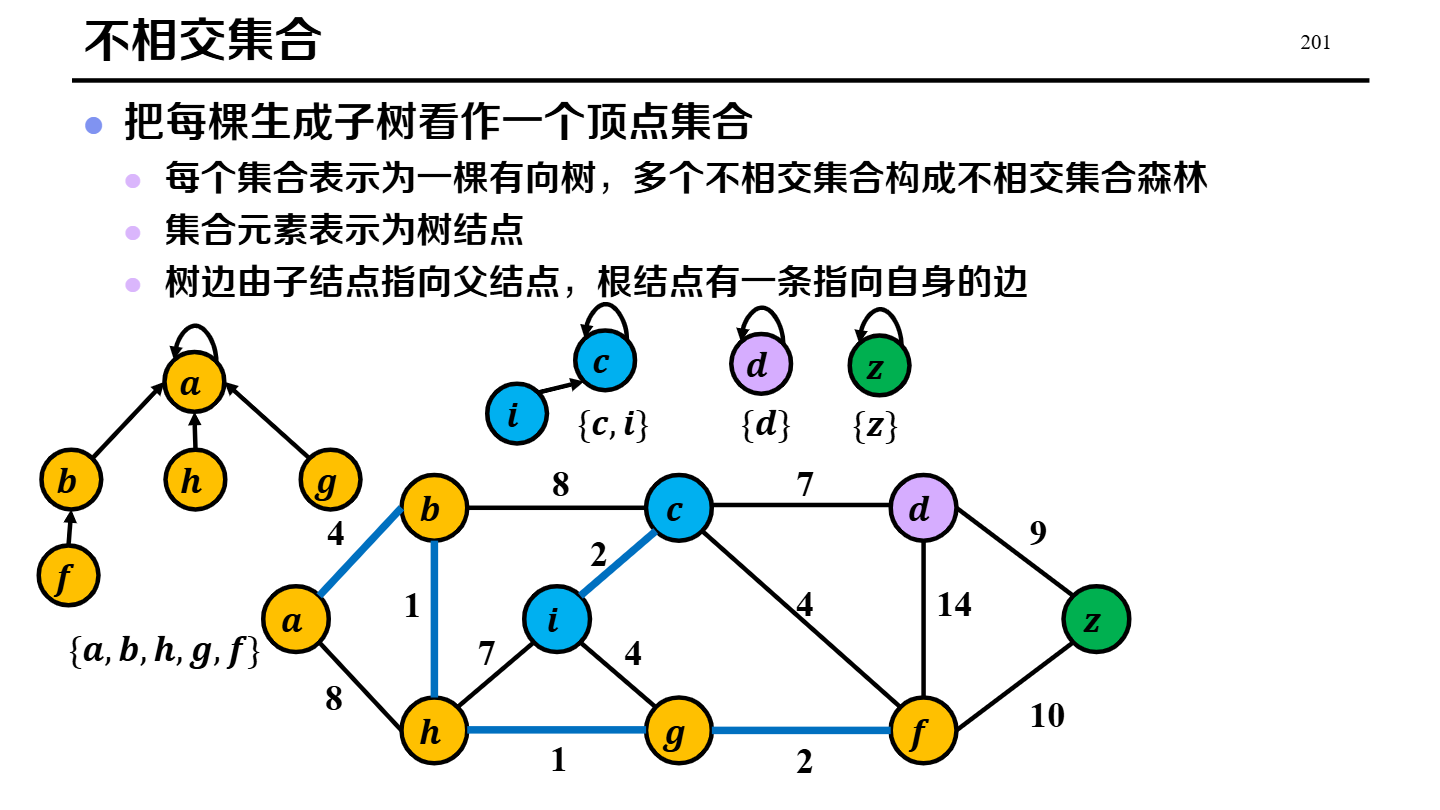
kruskal不相交集合思想.png — kruskal不相交集合思想.png（如文件名不同请修改）

不相交集合时间复杂度1.png — 不相交集合时间复杂度1.png（如文件名不同请修改）

不相交集合时间复杂度2.png — 不相交集合时间复杂度2.png（如文件名不同请修改）

不相交集合伪代码.png

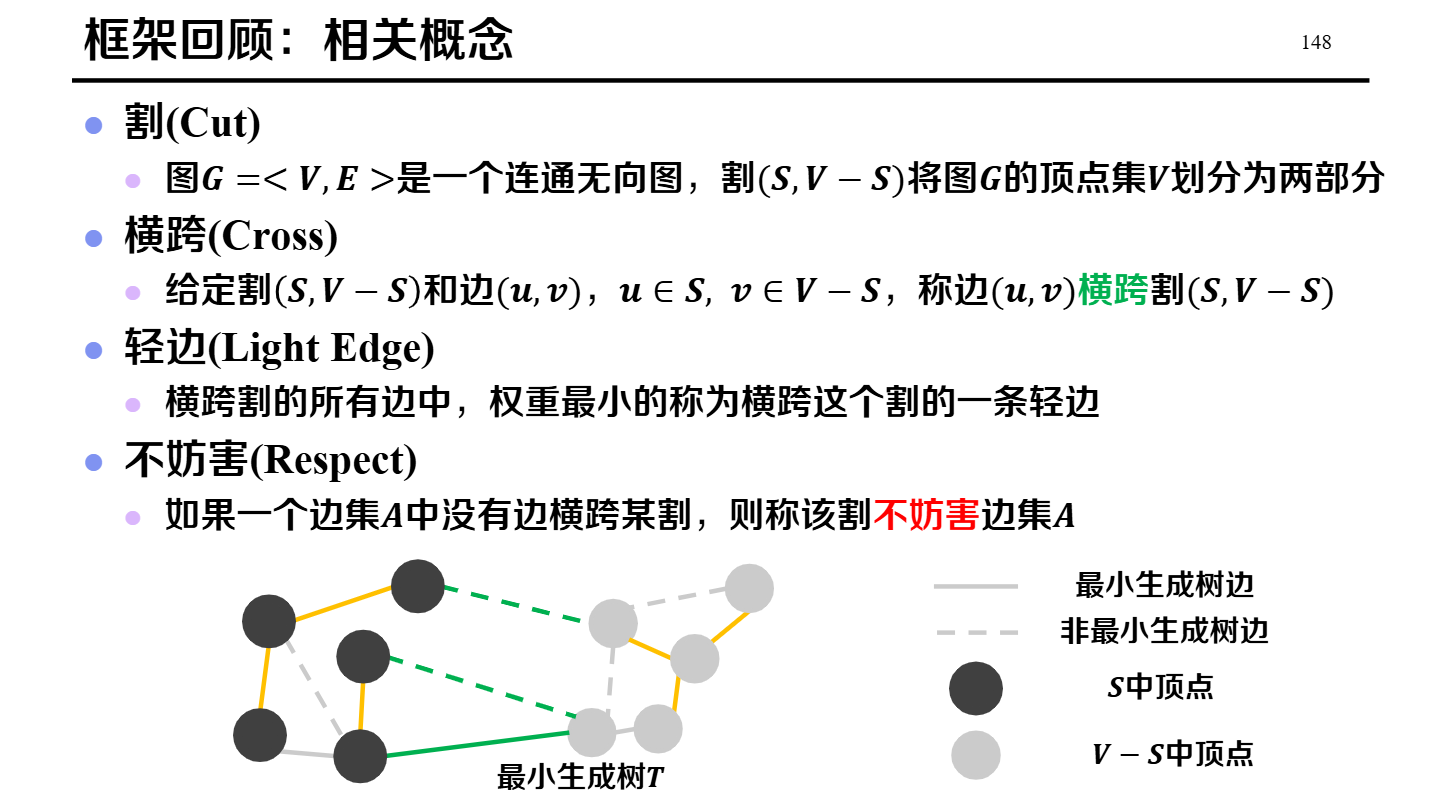
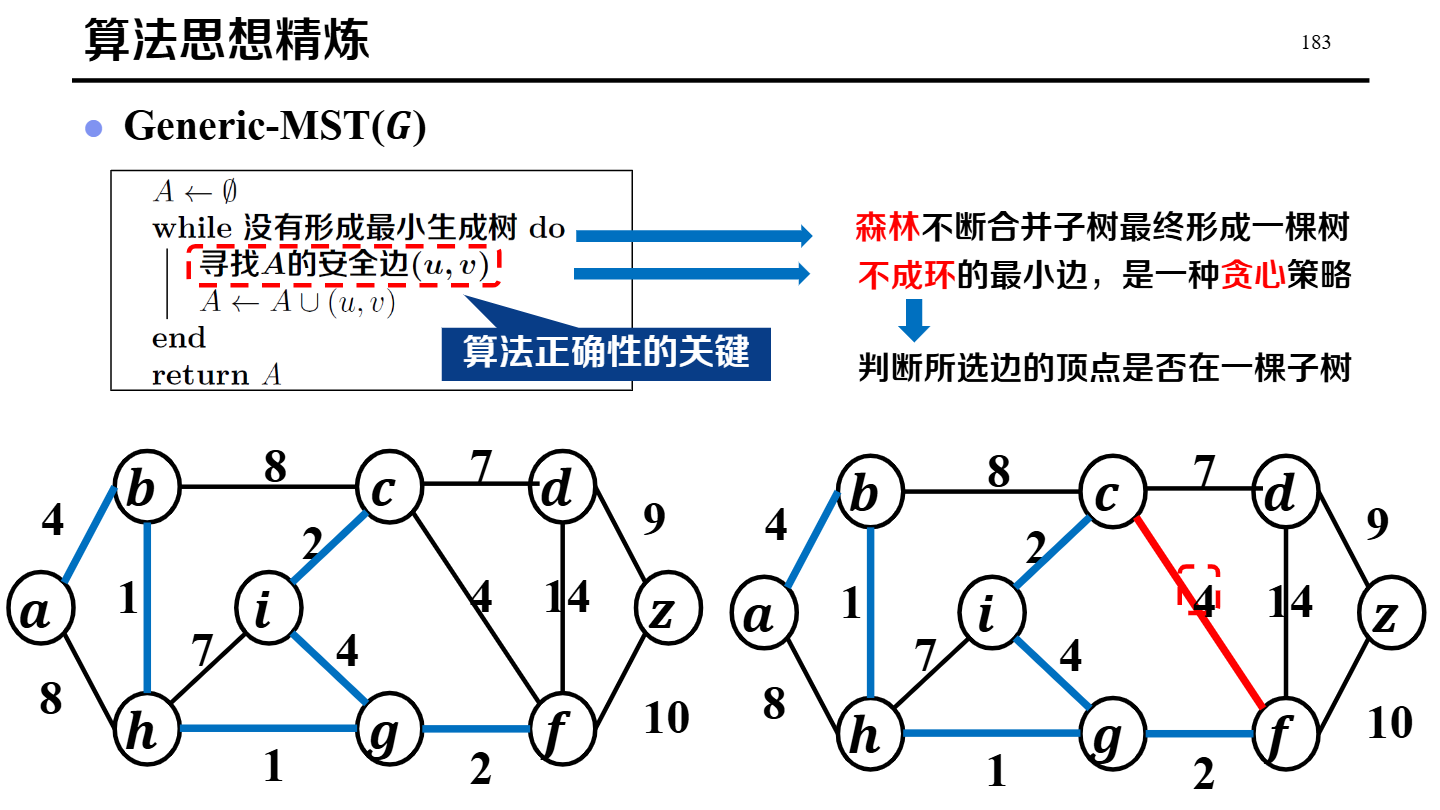
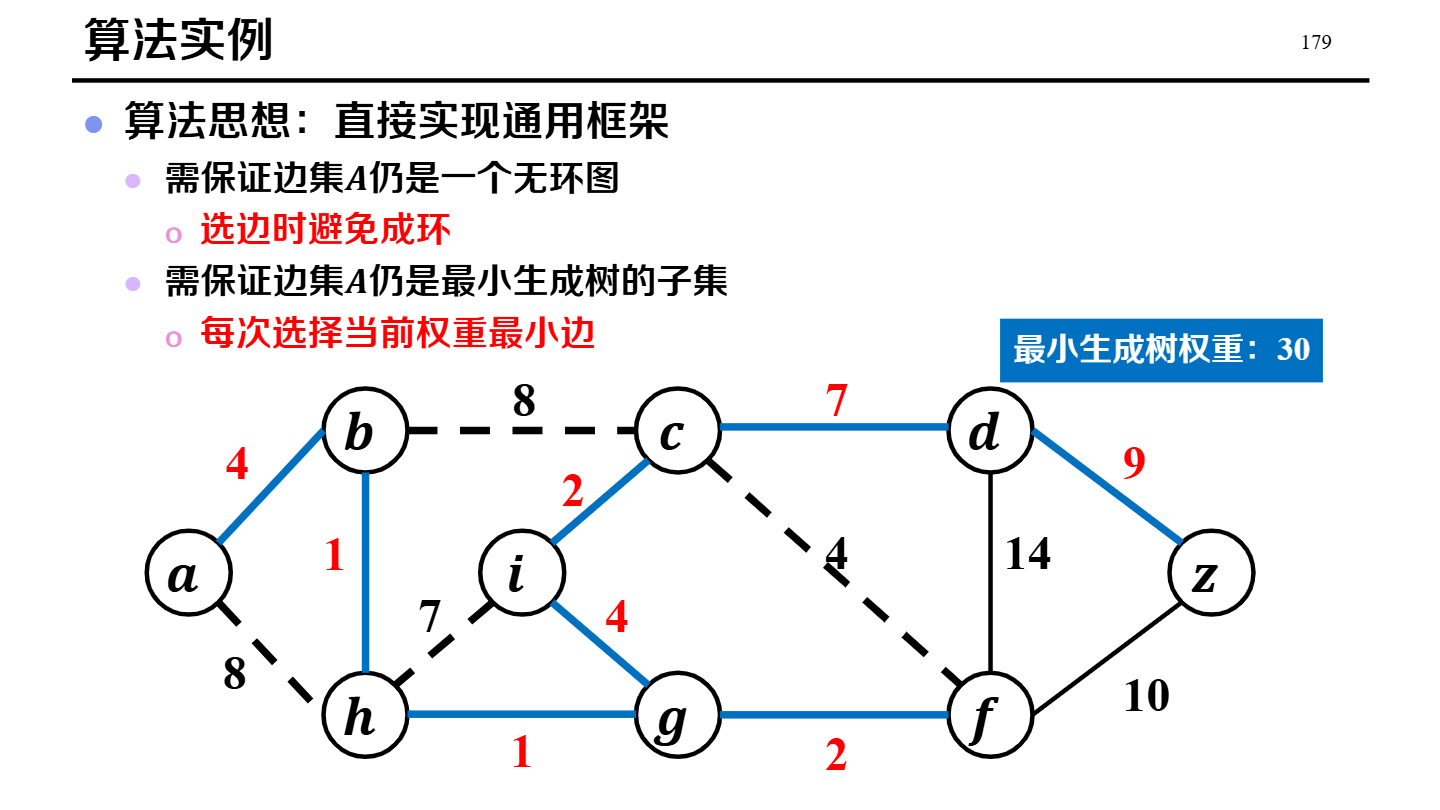
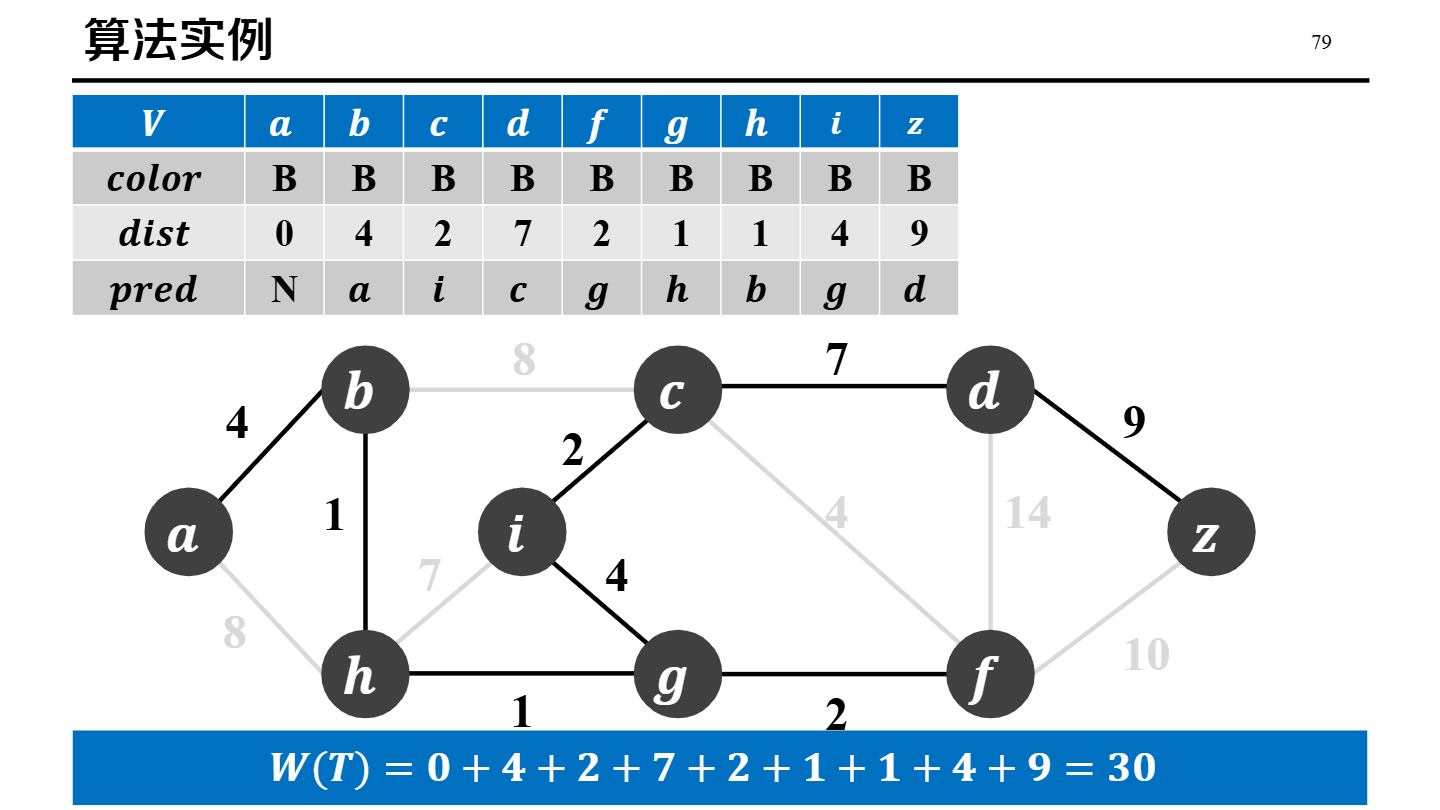
kruskal-prim比较.png

Prim

prim示例.png

prim复杂度.png

prim总结.png

prim初始化伪代码.png

prim执行伪代码.png

优先队列prim初始化伪代码.png

优先队列prim执行伪代码.png

递归方程式求解

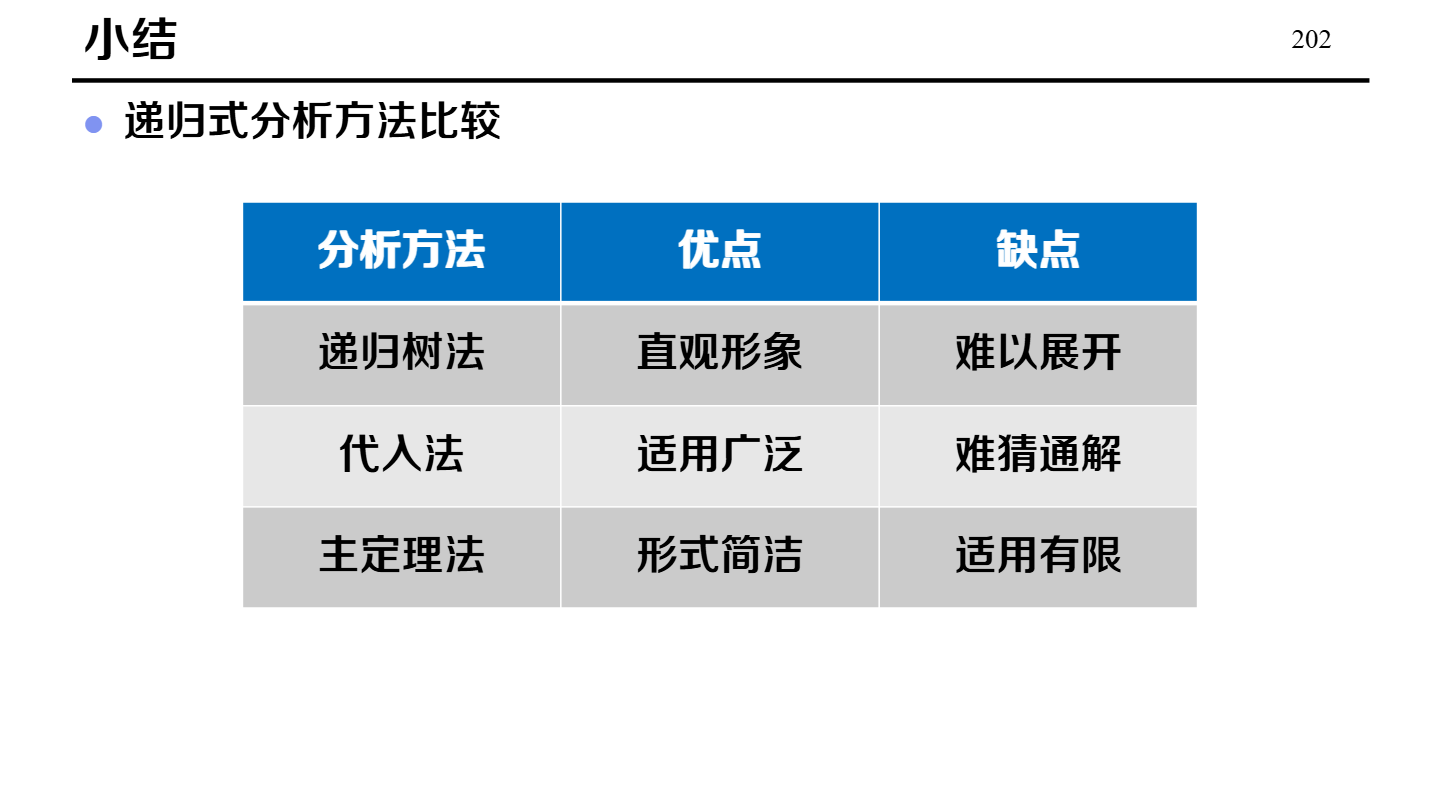
递归式分析方法比较.png

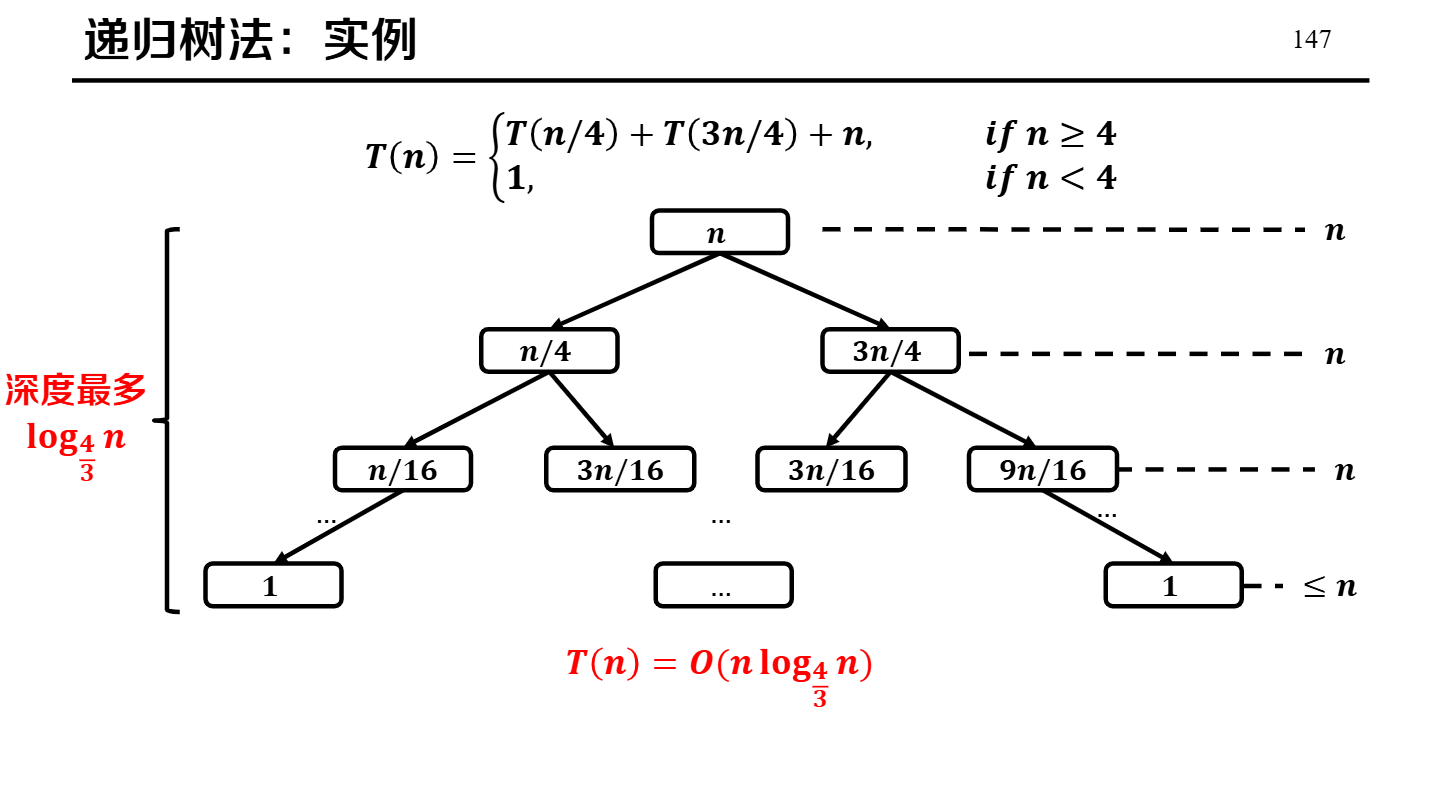
递归树法.png

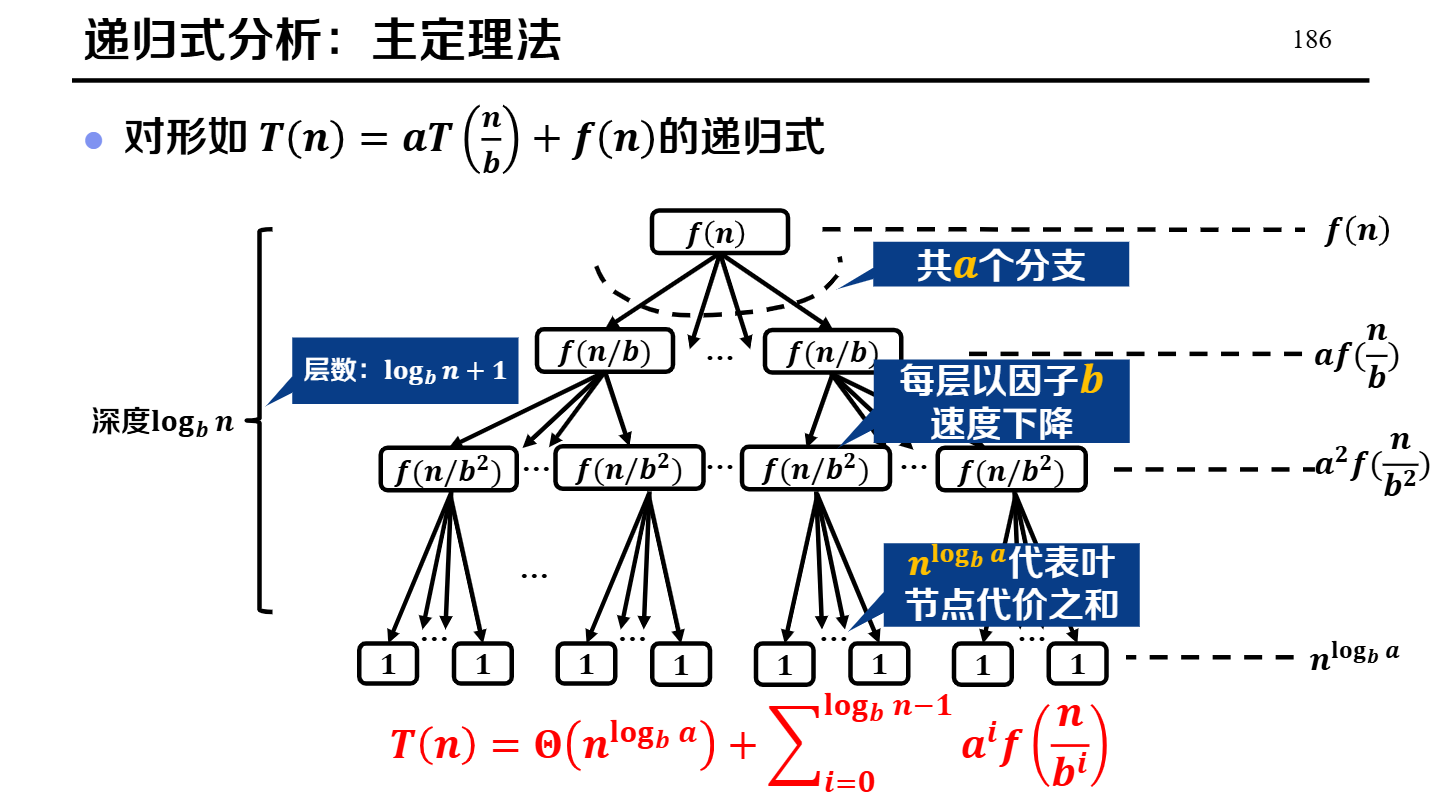
主定理法.png

主定理法化简.png

（可选）快速排序（额外）

如果你只要“五部分分类”，可以把这一节删掉。

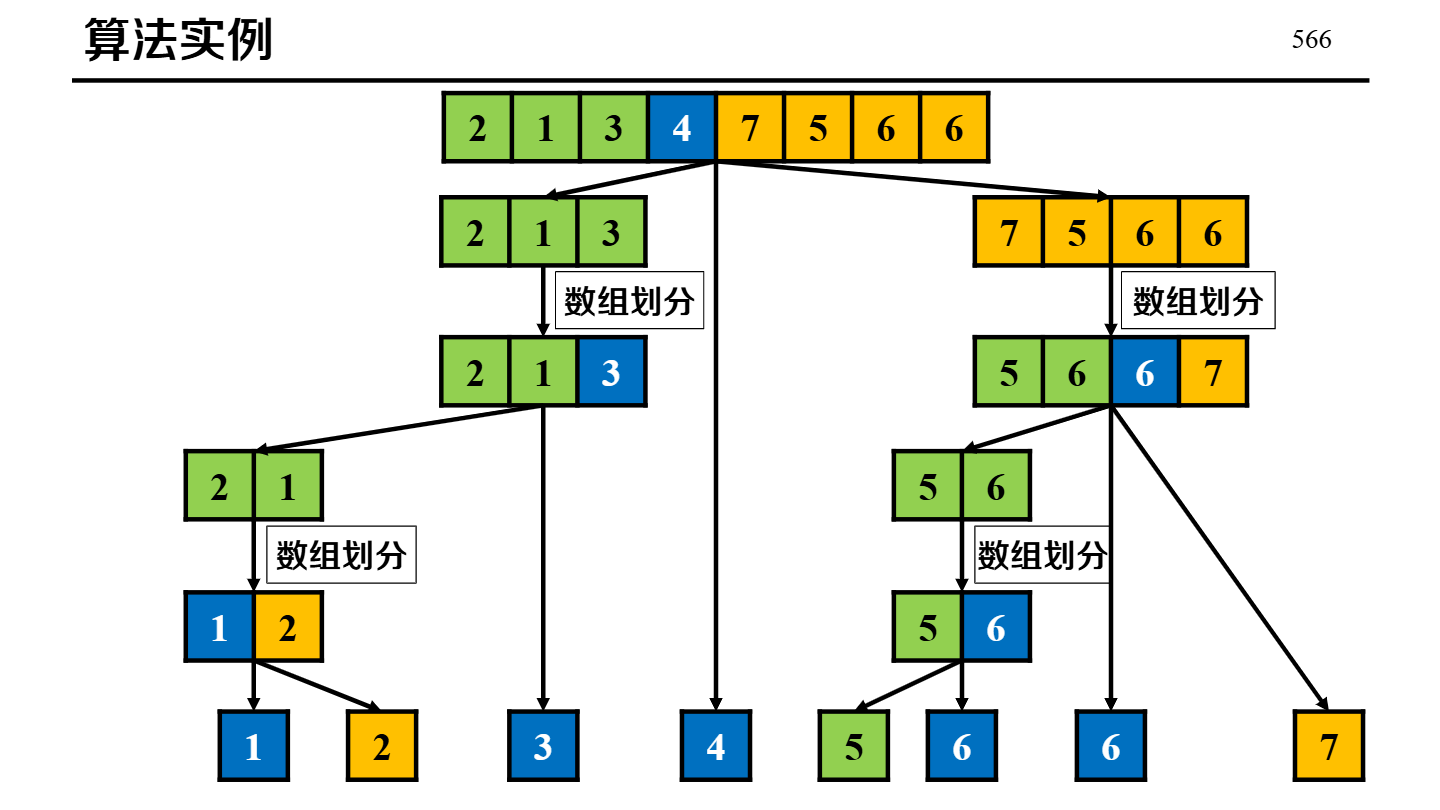
快速排序示例.png

快速排序数组划分.png

快速排序伪代码.png

快速排序最好情况.png

快速排序最坏情况.png

数组划分伪代码.png

2) 排序算法对比表

说明：此表按“思路、复杂度、稳定性、最优情况、最坏情况”组织。复杂度默认指时间复杂度（并补充空间复杂度）。

算法	思路	复杂度（时间/空间）	稳定性	最优情况	最坏情况
归并排序	分治：递归将数组二分，分别排序后进行“有序合并”。	时间：`O(n log n)` 空间：`O(n)`	稳定（合并时相等元素保持相对次序）	时间：`O(n log n)`	时间：`O(n log n)`
选择排序	每一轮从未排序区间中选择最小（或最大）元素，放到已排序区间末尾（交换）。	时间：`O(n^2)` 空间：`O(1)`	不稳定（交换可能改变相等元素顺序）	时间：`O(n^2)`	时间：`O(n^2)`
插入排序	维护前缀有序：将当前元素向左插入到合适位置（通过移动元素实现）。	平均时间：`O(n^2)` 空间：`O(1)`	稳定（相等元素不跨越）	（基本有序）时间：`O(n)`	（逆序）时间：`O(n^2)`
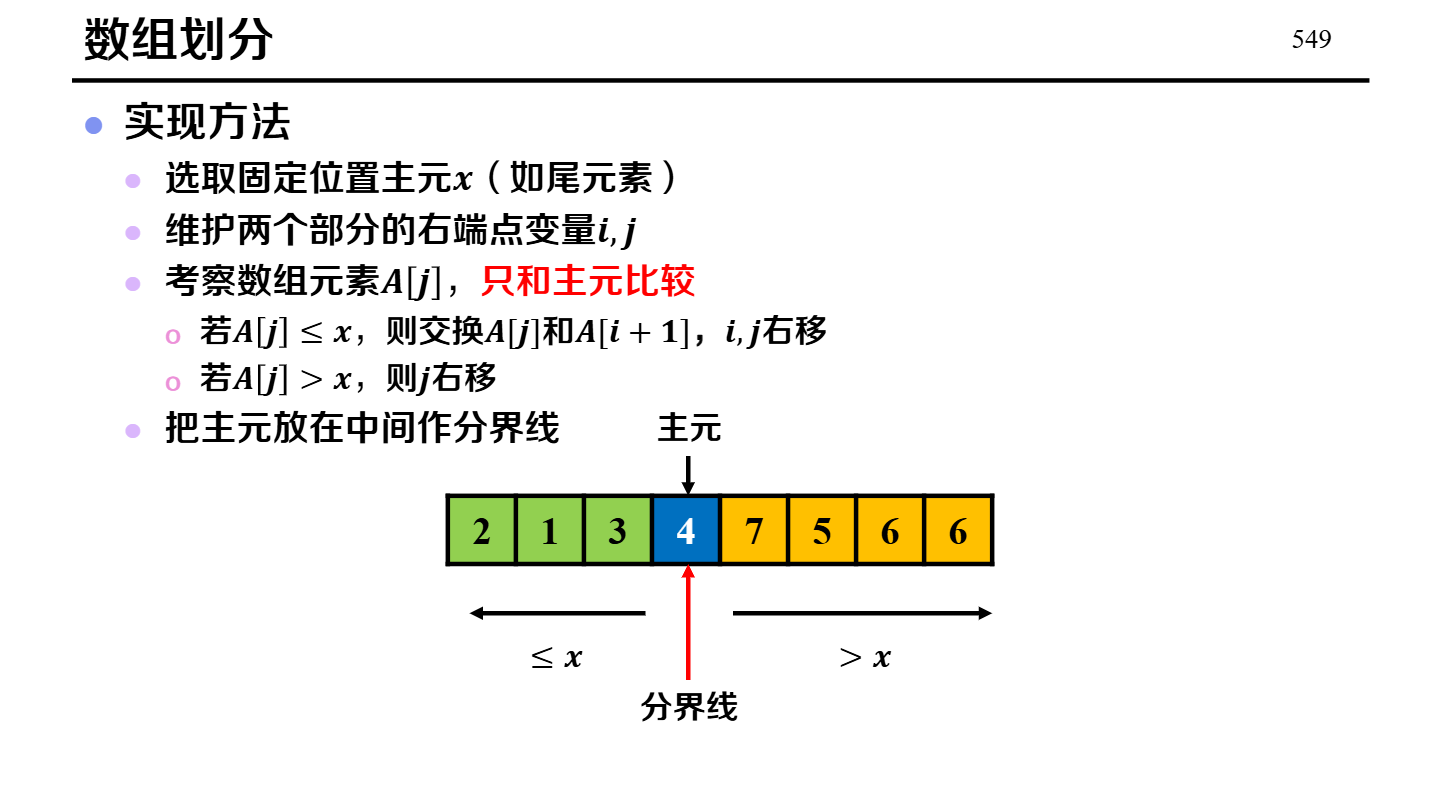
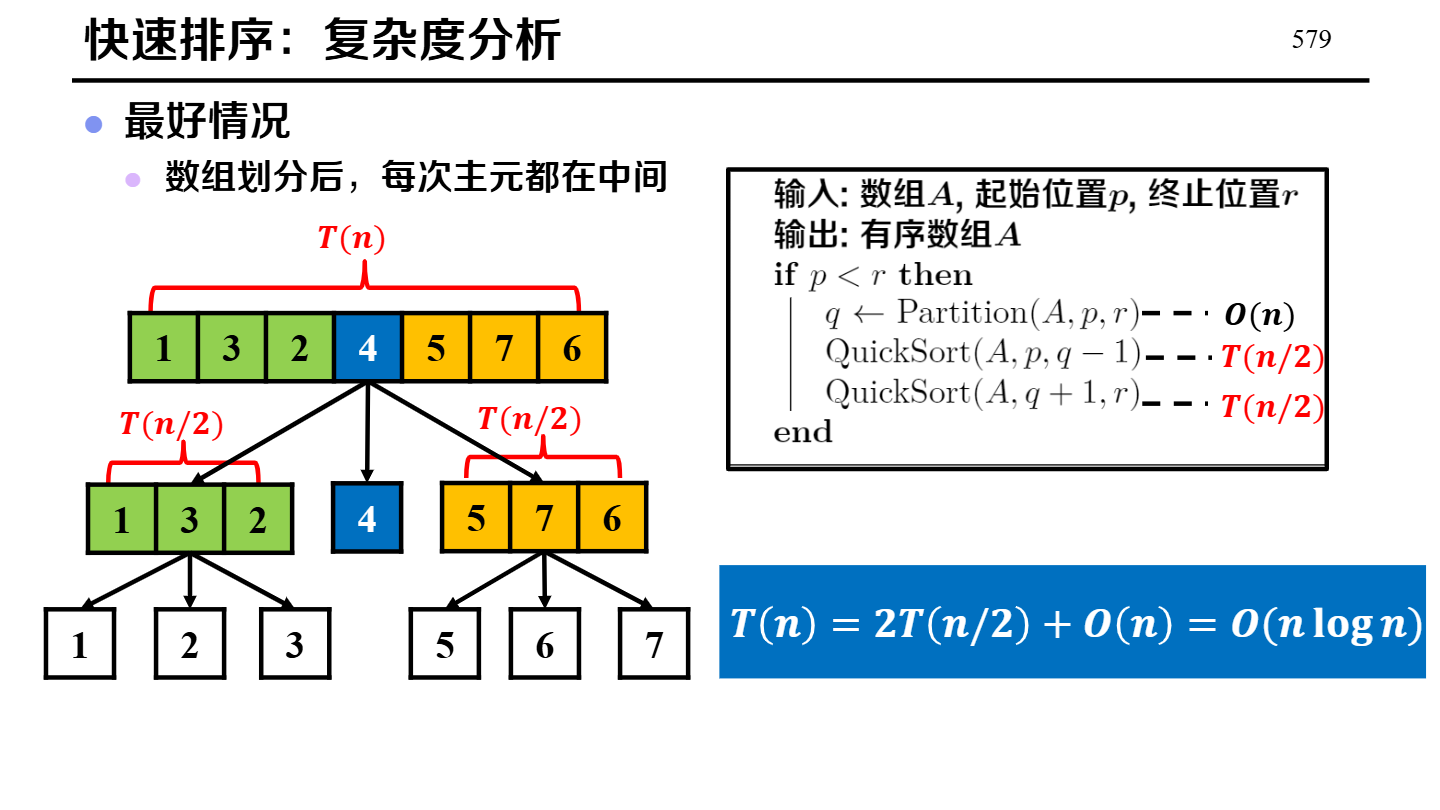
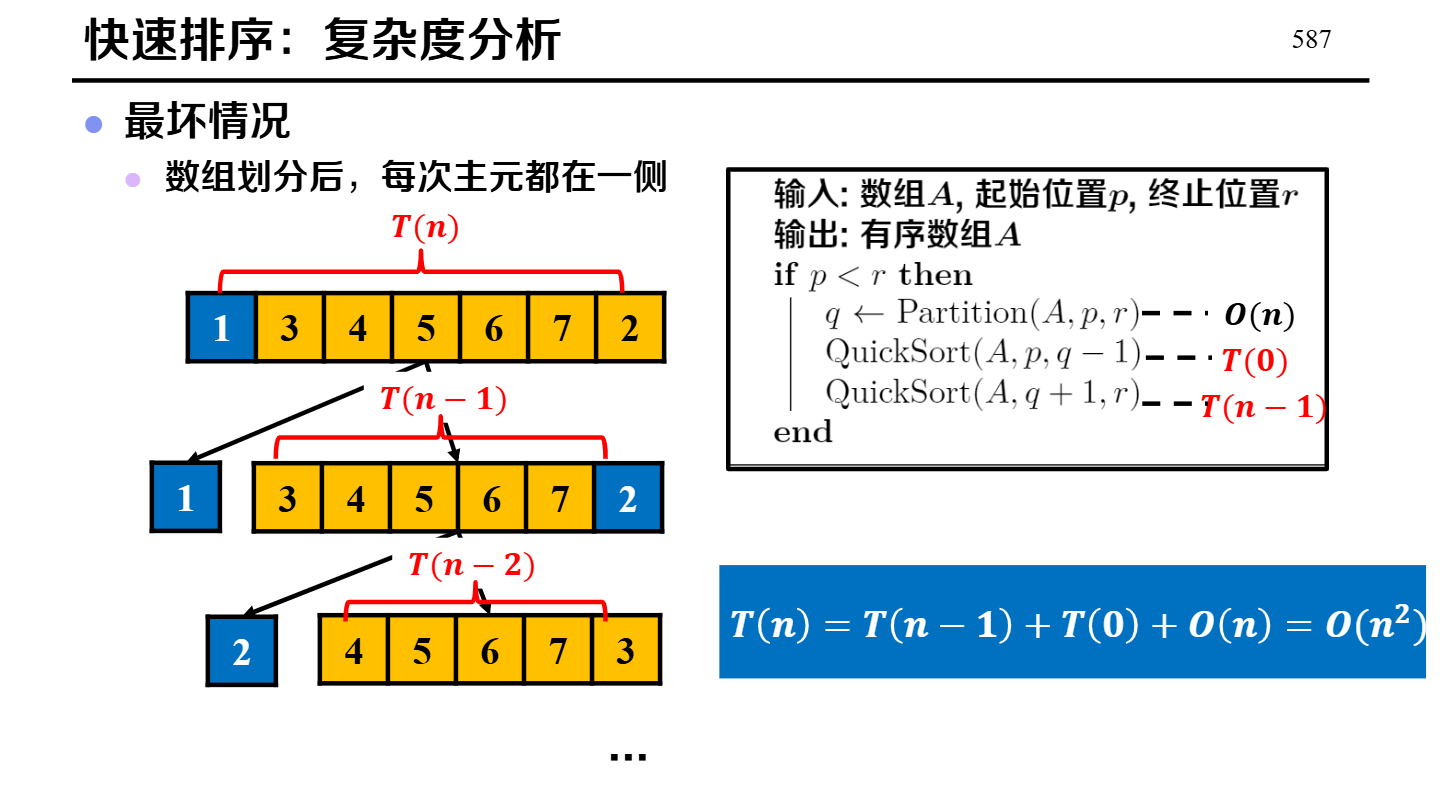
快速排序	分治：选枢轴 pivot，把数组划分为“小于 pivot”和“大于等于 pivot”（或相反）两部分，递归排序子区间。	平均时间：`O(n log n)` 空间：平均 `O(log n)`（递归栈），最坏 `O(n)`	不稳定（交换/划分会打乱相等元素）	（划分均匀）时间：`O(n log n)`	（极端不均匀，如已排序且选端点为枢轴）时间：`O(n^2)`

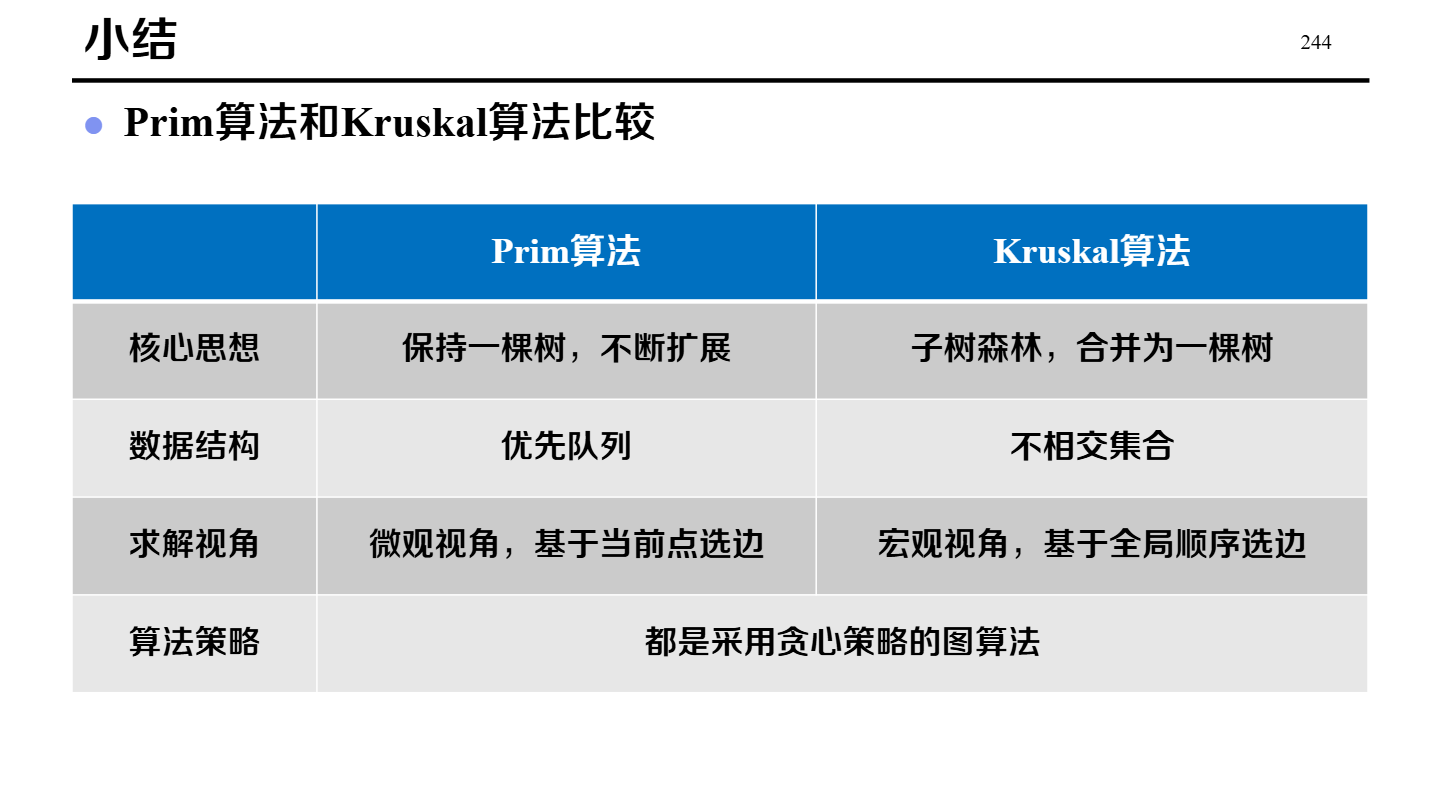
3) MST 两种算法对比表

说明：MST 一般不讨论“排序稳定性”那种稳定概念；这里“稳定性”列写为“不适用 / 可能多解（权值相同）”。

算法	思路	复杂度（常见实现）	稳定性
Kruskal	边的角度：将所有边按权值从小到大排序，依次尝试加入；若加入后成环则跳过（用并查集判断）。	排序：`O(E log E)` 并查集：近似 `O(E α(V))` 综上：通常写 `O(E log E)`	不适用（MST 无“稳定排序”概念）；当存在相同权值边时，可能得到不同但同权的 MST。
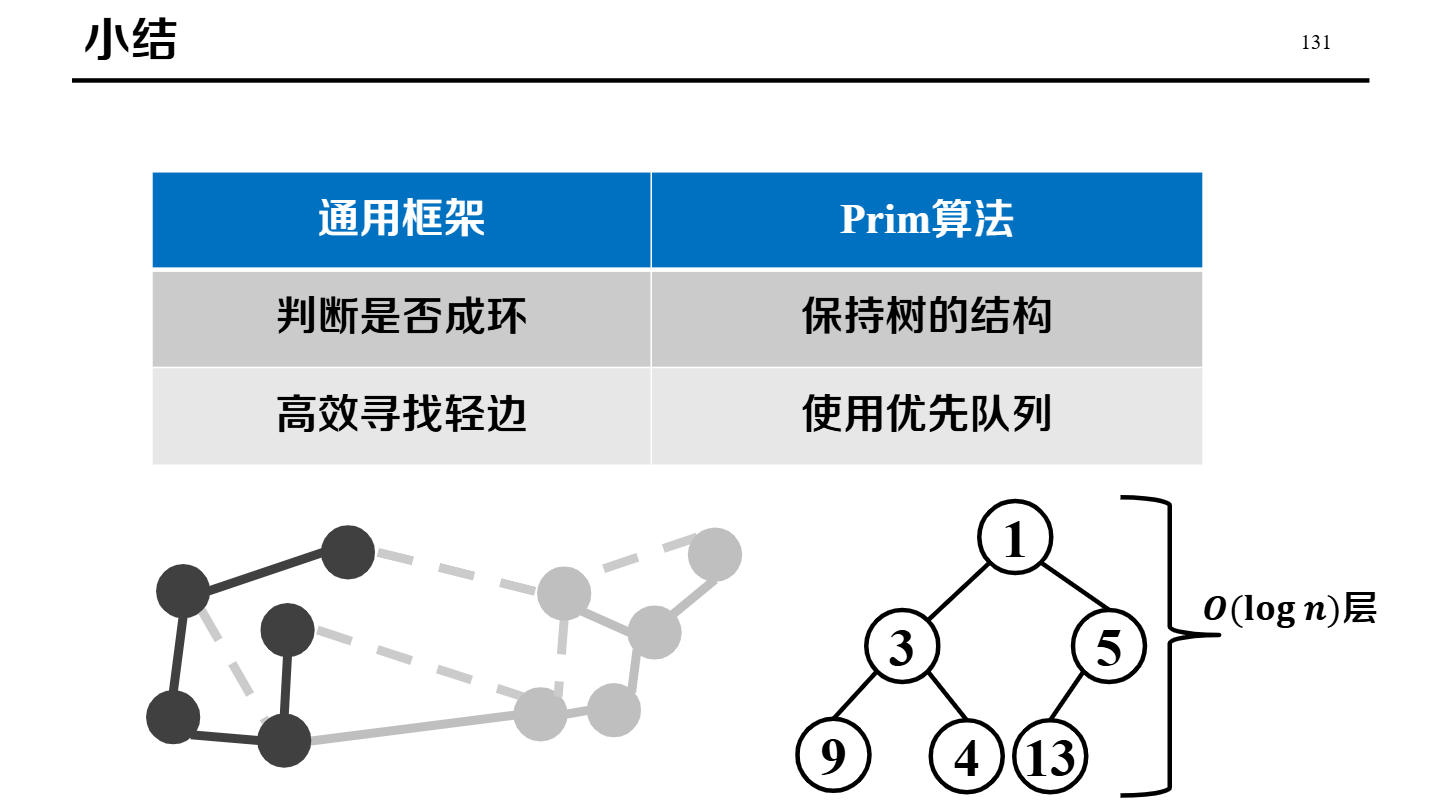
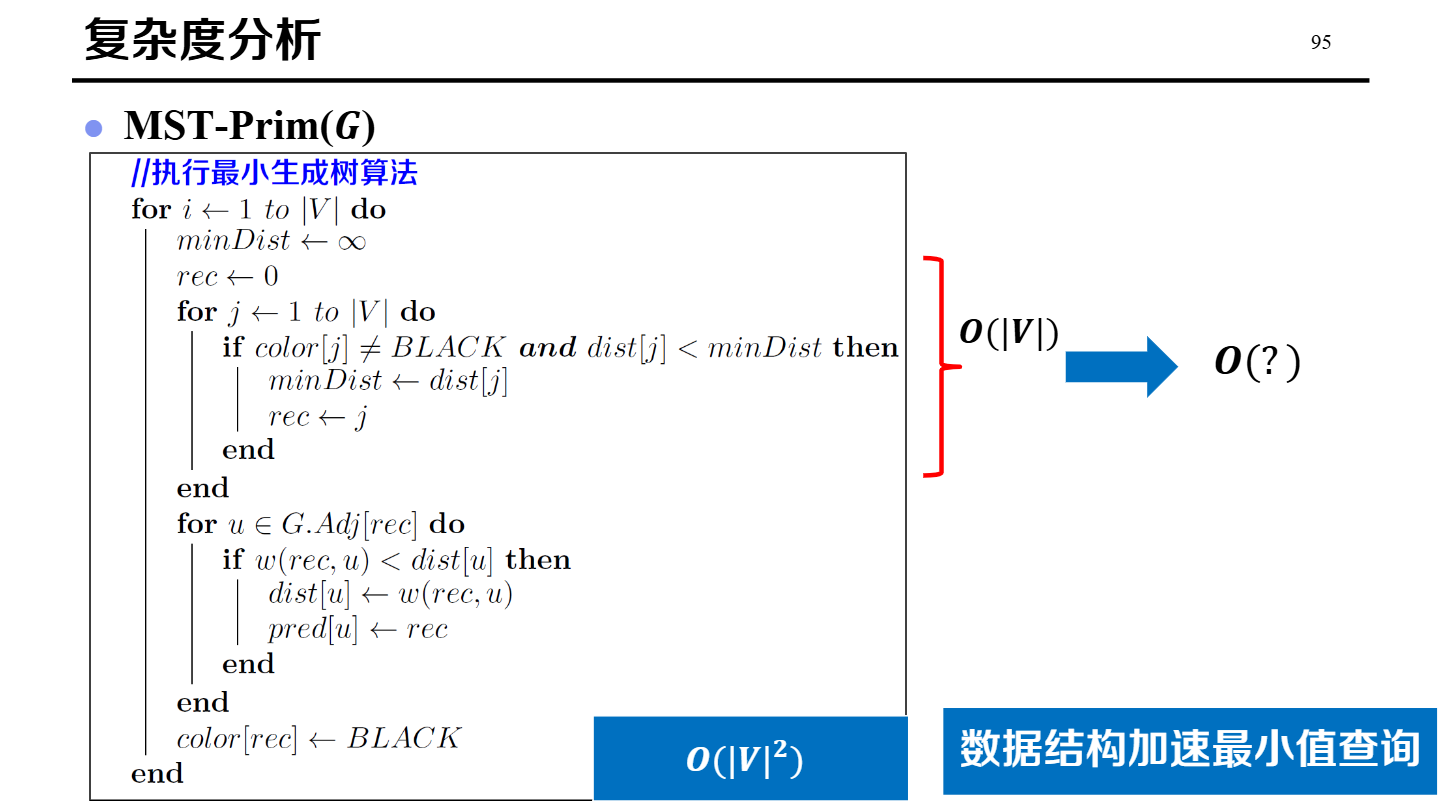
Prim	点的角度：从任意起点开始，每次选择一条“连接已选集合与未选集合”的最小权值边，把新顶点扩展进来。	二叉堆 + 邻接表：`O(E log V)` 邻接矩阵：`O(V^2)` （进阶）斐波那契堆：`O(E + V log V)`	不适用；同权边情况下可能多解（取边顺序不同会得到不同 MST）。